SVD는 특이값을 분해하는 것을 말함
특이값이란?
쉽게 말해, 고윳값에 루트를 씌운 값

교유 값과 고유 벡터?
- 정방 행렬 A를 선형 변환할 경우, 선형 변환 A에 의한 변환 결과가 자기 자신의 상수 배가 되는 0이 아닌 벡터를 고유 벡터라 하며, 상수에 해당되는 값을 고유 값이라고 함
- 다시 말해, 정방 행렬 A에 대해서 Aν=λν를 만족하는 0이 아닌 열 벡터를 고유 벡터, 상수 λ를 고유 값이라고 함
정방 행렬(Square matrix)
- 같은 수의 행과 열을 가지는 행렬
- n*n 행렬은 차수(order)가 n인 정방 행렬이라고도 하며, n차 정방 행렬이라고도 함
선형 변환과 추가 설명
- 선현 변환은 벡터에 사칙연산을 해주는 개념
- 위의 설명을 예시로, Aν라는 것은 '열벡터 ν에 선현 변환 A를 했음'이라고 표현
- 열 벡터 ν에 선현 변환 A를 한 결과가 열 벡터 ν의 상수 배(λ)와 동일하면, '선형 변환 A에 대하여 ν는 고유 벡터, λ는 고윳값이다'라고 표현
- 따라서 Aν=λν를 만족한다는 것은 벡터 ν에 대해 선형 변환 A를 했을떄, 벡터 ν의 방향은 변하지 않고 크기만 변했다는 것
- 즉, 어떠한 선형 변환 A를 했을 때, 크 크기만 변하고 방향이 변하지 않는 벡터가 있는가? 라는 질문에 '있다'인 경우는 고윳값과 고유 벡터가 존재한다고 할 수 있음
SVD( Singular Value Decomposition, 특이값 분해)
- 행렬 분해 방식 중 하나
- 행렬 분해(matrix decomposition)?행렬을 특정한 구조를 가진 다른 행렬의 곱으로 나타내는 것
- 행렬 분해의 목적선형 방정식의 해를 구하기 효율적인 행렬 계산 행렬의 특정 구조를 파악 하기정 방 행렬뿐만 아니라 행과 열의 크기가 다른 행렬에도 적용 가능
- SVD는 m*n 크기의 행렬 A를 m*m크기의 행렬 U와 m*n 크기의 ∑, 그리고 m * n 크기의 V^T로 분해
- 즉, A라는 행렬을 아래와 같이 만들고자 하는 것이 SVD임
수식으로 표현

그림으로 표현

1. U는 A*A^T의 고유벡터를고유 벡터를 열로 구성되며 직교 행렬임, U는 left singular vector A*A^T의 고유 벡터를 열로 구성된다?
- 특이 값 분해를 위한 고유값 분해를 위한 과정이라고 설명할 수 있음. 앞서 특이값 분해는 고윳값에 루트(√)를 씌운 값이라고 설명함
- 그렇다면 고유값 분해를 해야 하지만 SVD는 위 그림과 같이 m*n행렬이기 때문에 고윳값 분해가 불가능함 왜냐하면 고윳값 분해는 정방 행렬(정사각형 행렬)에서만 가능하기 때문임
- 따라서 (A_m*n) X (A_n*m)을 행렬곱셈후 정방 행렬을 만들고 고윳값과 고유 벡터를 구하는 것
A*A^T를 곱해서 고유값과 고유 벡터 구하는 과정

1.1 대각 행렬의 전치행렬은 자기 자신과 같기 때문에 아래와 같은 공식이 가능함

1.2. 정방 행렬 A에 대해서 Aν=λν를 만족하는 0이 아닌 열 벡터를 고유 벡터, 상수 λ를 고유 값인 공식에λ, A*A^T의 0이 아닌 고윳값 고유 벡터 ν을 대입하면 아래와 같은 식이 성립

1.3. 1번식에서 양변에 U를 곱하면 아래와 같은 식이 성립




2. 또한 V는 A^T * A의 고유 벡터를 열로 구성되며 직교 행렬임, right singular vector라고도 불림

3. ∑는 직사각 대각 행렬이며, 대각 원소 값이 바로 행렬 A의 특이값
- ∑의 대각원소는 A*A^T 혹은 A^T*A의 고윳값의 루트와 같음, 고윳값에 루트를 씌웠기 때문에 특이값
SVD와 TruncatedSVD 차이점
SVD의 대각 행렬 ∑에서 비 대각 부분과 대각 원소(특이값)에서 0인 부분을 모두 제거하고 그에 대응되는 U와 V의 원소
도 함께 제거해 차원을 줄인 형태가 TruncatedSVD즉, SVD의 대각 행렬 ∑에서 0인 부분을 모두 제거하고 t개의 열만 추출
후 U와 V를 수정한 것이 SVD임
그림으로 표현할 경우
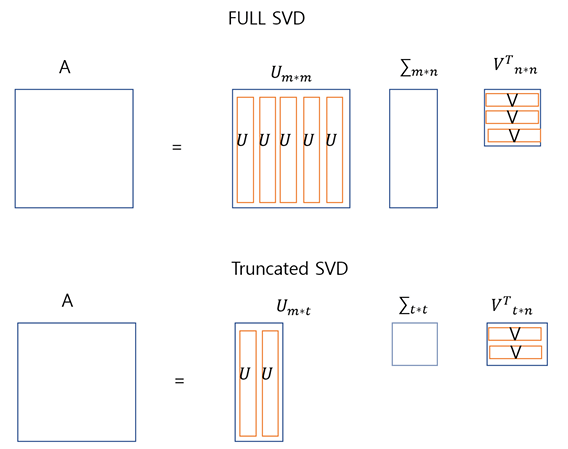
0인 부분을 제거하는 특성때문에 TruncatedSVD는 분해를 하고 원소를 잃어버리기 때문에 원본 행렬 A로 원복이 불가함
반대로 SVD는 모든 원소가 남아있기때문에 원본 행렬 A로 원복이 가능함
남는 의문점 해결
- "SVD가 정방행렬이 아닌 경우 사용할 수 있는 것과 특이값을 분해하는 과정은 알겠는데, 그래서 분해하는 이유가 뭔가?"입니다. SVD가 특이값을 분해하는 이유이면서 SVD의 아이디어임
1. 아래 그림과 같이 직교하는 두 벡터가 있다고 할 때, 두 벡터에 대해 어떤 선형변환을 아래 그림과 같이 함
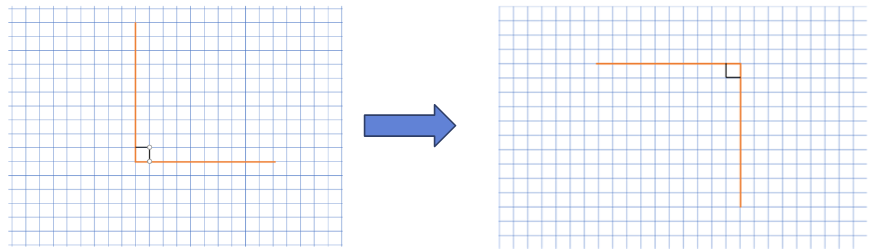
2. 만약 선형 변환을 했음에도, 여전히 두 벡터가 직교하고 있다면 이 벡터들이 특정한 의미를 가질 것이다라는 아이디어임
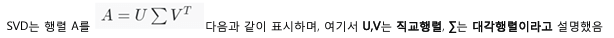
직교 행렬 : 좌표공간에서 회전 행렬을 의미
- 회전 행렬 : 점 또는 도형을 회전시켜주는 행렬 (ex), x축 회전,)
대각 행렬은 좌표공간에서 크기 행렬을 의미
- 크기 행렬 : 점 또는 도형의 크기를 확대시키는 행렬 (x →2x)
결론적으로 SVD는 V^T에 의해 회전하고, ∑로 크기 변환 후 U에 의해 회전시켜 특이값을 얻음
즉, SVD가 얻는 특이값이란 고윳값의 루트 값이자 행렬로 표현되는 선형 변환의 크기 변환과 회전 변환을 거친 값으로 설명이 가능함
참고한 블로그(Reference)
머신러닝 - 차원 축소 (PCA, LDA, SVD, NMF)
안녕하세요~ 오늘 알아볼 것은 차원축소입니다. 실제로 우리가 데이터를 받았을 때, 여러가지 피쳐들로 이...
blog.naver.com
[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
활용도 측면에서 선형대수학의 꽃이라 할 수 있는 특이값 분해(Singular Value Decomposition, SVD)에 대한 내용입니다. 보통은 복소수 공간을 포함하여 정의하는 것이 일반적이지만 이 글에서는 실수(real
darkpgmr.tistory.com
[선형대수] 특이값 분해(Singular Value Decomposition)의 의미
특이값 분해(Singular Value Decompostion)의 개념과 의미
losskatsu.github.io
머신러닝 - 20. 특이값 분해(SVD)
이번 장에서는 특이값 분해(SVD)에 대해 알아보겠습니다. 고유값 분해에 대해 알고 있어야 특이값 분해를 이해할 수 있습니다. 고유값 분해를 잘 모르시는 분은 이전 장을 참고해주시기 바랍니다
bkshin.tistory.com
'Study > ML 공부' 카테고리의 다른 글
| Few shot learning? Meta Learning? (1) | 2022.12.12 |
|---|---|
| Bayesian Optimization(베이지안 최적화)란? (0) | 2022.08.14 |
| [Study] AdaBoosting vs GradientBoosting 차이점 (0) | 2022.04.17 |
| [Study] ExtraTreesClassifier vs RandomForestClassifier 차이점 (0) | 2022.04.03 |
| 원핫인코더 fit은 한번만 할 껀데? (feat.check_is_fitted, try-except , if - else) (0) | 2022.03.23 |



