Book Title : Introduction to Machine Learning with Python
- 파이썬 라이브러리를 활용한 머신러닝 -
지은이 : 안드레아스 뮐러, 세라 가이도
옮긴이 : 박해선
출판사 : 한빛미디어
코드 출처
https://github.com/rickiepark/introduction_to_ml_with_python
GitHub - rickiepark/introduction_to_ml_with_python: 도서 "[개정판] 파이썬 라이브러리를 활용한 머신 러닝"의
도서 "[개정판] 파이썬 라이브러리를 활용한 머신 러닝"의 주피터 노트북과 코드입니다. Contribute to rickiepark/introduction_to_ml_with_python development by creating an account on GitHub.
github.com
개요
책을 읽고 줄거리를 요약
이미 알고 있는 부분은 빨리 넘어가고 모르는 부분 위주로 요약
3.4.1 주성분 분석(PCA)
- 특성들이 통계적으로 상관관계가 없도록 데이터셋을 회전시키는 것
- 주성분의 일부만 남기는 차원 축소 용도로 사용 가능
- 가장 널리 사용되는 분야는 고차원 데이터셋의 시각화
- 그래프의 두 축을 해석하기 쉽지 않음
유방암 데이터셋에 PCA 적용
cancer = load_breast_cancer()
from sklearn.preprocessing import StandardScaler
# PCA 적용전 스케일링
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
# PCA 변환을 학습하고 적용하는것은 간단
# 1. 객체 생성
# 2. fit 을 사용해 주성분 찾기
# 3. transform 사용해 데이터 회전및 차원 축소
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
# PCA 모델 생성
pca.fit(X_scaled)
# 데이터 변환
X_pca = pca.transform(X_scaled)
print("원본 데이터 :", str(X_scaled.shape))
print("축소 데이터 :", str(X_pca.shape))
# 원본 데이터 : (569, 30)
# 축소 데이터 : (569, 2)시각화
plt.figure(figsize = (8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(["maliggnant", "benign"], loc ="best")
plt.gca().set_aspect("equal")
plt.xlabel("first pca")
plt.ylabel("second pca")
고유얼굴 특성 추출
- - PCA는 특성 추출에도 이용
PCA를 이용해서 얼굴 이미지 특성 추출하기

간단하게 최근접 이웃 분류기를 사용해 분류, 정확도가 22%로 매우 낮음
# 얼굴 인식이라 하면 통상적으로 새로운 얼굴 이미지가 데이터 베이스에 있는 기존 얼굴 중 하나에 속하는지 찾는 작업
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
from sklearn.model_selection import train_test_split
mask = np.zeros(people.target.shape, dtype =np.bool)
for t in np.unique(people.target):
mask[np.where(people.target == t)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
X_people = X_people /255.0
X_train, X_test, y_train, y_test = train_test_split(X_people, y_people, stratify = y_people, random_state =1)
knn = KNeighborsClassifier(n_neighbors = 1)
knn.fit(X_train, y_train)
print("1-neighbor test score : ", knn.score(X_test, y_test))
# 1-neighbor test score : 0.2248062015503876
PCA 화이트닝 옵션을 상해서 주성분의 스케일이 같아지도록 조정
이것은 StandardScaler를 적용하는 것과 동일

PCA 객체를 훈련 데이터로 학습시켜 데이터셋을 변환하여 최근접 이웃 분류기로 이미지 분류
정확도가 22% → 31% 향상
from sklearn.decomposition import PCA
pca = PCA(n_components = 100, whiten =True, random_state = 0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
knn = KNeighborsClassifier(n_neighbors = 1)
knn.fit(X_train_pca, y_train)
print("1-neighbor test score : ", knn.score(X_test_pca, y_test))
# 1-neighbor test score : 0.33527131782945735
3.4.2 비음수 행렬 분해(NMF)
- Non-negative matrix factorization
- 특성을 뽑아내는 또 다른 비지도 학습 알고리즘
- 차원 축소
- PCA는 데이터 분산이 가장 크고 수직인 성분을 찾았다면 NMF는 음수가 아닌 성분과 계수 값을 찾음, 즉 주성분과 계수가 모두 0보다 크거나 같아야 함
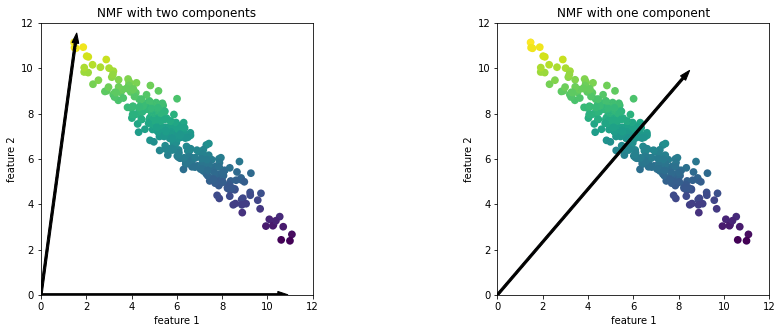
예제 데이터에 NMF 적용한 결과
- 왼쪽은 성분이 둘인 NMF, 데이터셋의 모든 포인트를 양수로 이뤄진 두 개의 성분으로 표현
- 오른쪽은 성분이 한개
또 다른 패턴 추출 알고리즘
- 독립 성분 분석(ICA)
- 요인 분석(FA)
- 희소 코딩(sparse coding)
3.4.3 t-SNE를 이용한 매니폴드 학습
- 매니폴드 학습 알고리즘이라고 하는 시각화 알고리즘들은 복잡잔한 매핑을 만들어 더 나은 시각화를 재공
- 특히 t-SNE 많이 사용
- 3개 이상의 특성을 뽑는 경우는 거의 없음
- 테스트 세트에는 적용할 수 없고, 단지 훈련한 데이터만 변환이 가능하여 지도 학습용으로는 거의 사용하지 않음
t-SNE의 아이디어
- 데이터 포인트 사이의 거리를 가장 잘 보존하는 2차원 표현을 찾는 것
- 데이터 포인트를 2차원에 무작위로 표현한 후 원본 특성 공간에서 가까운 포인트는 가깝게, 멀리 떨어진 포인트는 멀어지게 만듦
손글씨 숫자 데이터셋에 분류

- 대부분 많은 숫자가 겹쳐있음
t_SNE 적용
from sklearn.manifold import TSNE
tsne = TSNE()
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize = (10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color = color[digits.target[i]],
fontdict = {'weight': 'bold', 'size' : 9})
'Study > Introduction to ML with python - 한빛' 카테고리의 다른 글
| [Book] 4. 비지도학습과 데이터 전처리 - (1) (0) | 2022.02.25 |
|---|---|
| [Book] 3. 비지도학습과 데이터 전처리 - (3) (0) | 2022.02.20 |
| [Book] 3. 비지도학습과 데이터 전처리 - (1) (0) | 2022.02.15 |
| [Book] 2. 지도학습 - (2) (0) | 2022.02.13 |
| [Book] 1. 소개 (0) | 2022.02.06 |



