개요
책을 보고 공부한 내용을 정리합니다.
딥러닝 텐서플로 교과서
- 저자 서지영님
- 길벗 출판사
코드 출처
https://github.com/gilbutITbook/080263
GitHub - gilbutITbook/080263
Contribute to gilbutITbook/080263 development by creating an account on GitHub.
github.com
[Book]3. 머신러닝 핵심 알고리즘
3.1 지도 학습
지도 학습 : 정답을 컴퓨터에 미리 알려주고 데이터를 학습시키는 방법
- 지도 학습 종류 : 분류, 회귀
- 분류 : 주어진 데이터를 정해진 범주에 따라 분류
- 회귀 : 데이터들의 특성을 기준으로 연속된 값을 그래프로 표현하여 패턴이나 트렌드 예측
3.1.1 K-최근접 이웃
- 분류
- 직관적, 사용 쉬움
- 새로운 입력을 받았을 때, 기존 클러스터에서 모든 데이터와 인스턴스 기반 거리를 측정한 후 가장 많은 속성을 가진 클러스터에 할당하는 분류 알고리즘

# 최적의 K값 찾아보기
# k값을 1~ 10 까지 돌려보기
k = 10
acc_array = np.zeros(k)
for k in np.arange(1, k+1, 1): # 그냥 1부터 10이랑 같은거
classifier = KNeighborsClassifier(n_neighbors = k).fit(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = metrics.accuracy_score(y_test, y_pred)
acc_array[k-1] = acc
max_acc = np.amax(acc_array)
acc_list = list(acc_array)
k = acc_list.index(max_acc)
print("정확도", max_acc, "으로 최적의 k는", k+1)
3.1.2 서포트 벡터 머신
- 분류
- 커널만 적절히 선택한다면 정확도가 상당히 좋음
- 텍스트 분류할 때도 많이 사용
- 분류를 위한 기준선을 정의하는 모델
- 분류되지 않은 새로운 데이터가 나타나면 결정 경계(기준선)를 기준으로 경계의 어느 쪽에 속하는 분류

서포트 벡터 머신 - 결정 경계는 데이터가 분류된 클래스에서 최대한 멀리 떨어져 있을 때 성능이 좋음
- 마진은 결정 경계와 서포트 벡터 사이의 거리
- 서포트 벡터? 아무튼 워라벨님의 SVM 정리
svm = SVC(kernel = 'linear', C= 1.0, gamma = 0.5)
svm.fit(X_train, y_train)
predictions = svm.predict(X_test)
score = metrics.accuracy_score(y_test, predictions)
print("정확도 :{0:f}".format(score))- SVM은 선형 분류와 비선형 분류

- 비선형 문제를 해결하는 기본적인 방법은 저차원 데이터를 고차원으로 보내는 것
- 수학적 계산이 많이 필요하기 때문에 성능에 문제를 줌 -> 해결하기 위해 '커널 트릭' 도입
커널 트릭
선형 모델에 : 선형 커널
비선형 커널 : '가우시안 RBF 커널' , '다항실 커널'
수학적 기교를 이용하는 것으로, 벡터 내저을 계산한 후, 고차원으로 보내서 연산량 줄임
3.1.3 결정 트리
- 분류
- 이상치가 많은 값으로 구성된 데이터셋을 다룰 때 좋음
- 데이터를 1차로 분류 후 -> 영역의 순도 증가 -> 불순도, 불확실성 가소하면서 학습
엔트로피
- 확률 변수의 불확실성을 수치로 나타낸 것
- 높으면 불확실성이 높은 것
지니 계수
- 불순도 측정 지표
- 지니계수는 원소 n개 중에서 임의로 두 개 추출했을 때, 두 개가 서로 다른 그룹에 속해 있을 확률
- 높을수록 데이터가 분산되어 있음을 의미
# 모델 새성
model = tree.DecisionTreeClassifier()
model.fit(X_train, y_train)
# 예측
y_predict = model.predict(X_test)
# 정확도
accuracy_score(y_test, y_predict)3.1.4 로지스틱 회귀와 선형 회귀
- 회귀란 변수가 두 개 주어졌을 때 한 변수에서 다른 변수를 예측 Or 두 변수의 관계를 규명하는 데 사용
- 독립 변수 : 영향을 미칠 것으로 예상되는 변수
- 종속 변수 : 영향을 받을 것으로 예상되는 변수
로지스틱 회귀
- 분류
- 분석 대상이 두 집단 이상으로 나누어진 경우 사용
- 최대 우도 법 사용
# 로지스틱 모델 객체 생성
logisticRegr = LogisticRegression()
logisticRegr.fit(X_train, y_train)선형 회귀
- 분류
- 독립 변수와 종속 변수가 선형 관계를 가질 때 사용하면 유용
- 단순 선형 회귀 : 독립 변수 하나
- 다중 선형 회귀 : 독립 변수 두 개 이상
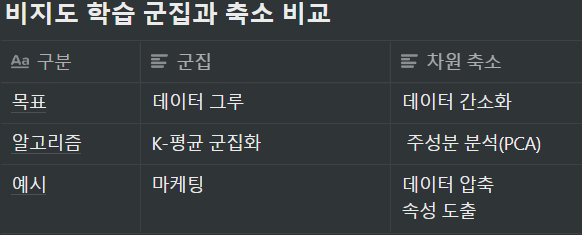
3.2 비지도 학습
- 정답이 없는 상태에서 훈련시키는 방식
- 군집과 차원 축소가 있음
- 군집은 각 데이터의 유사성(거리)을 측정 후 유사성이 높은(거리가 짧은) 데이터끼리 분류
- 차원 축소는 차원을 나타내는 특성을 줄여서 데이터를 줄이는 것
K-평균 군집화
학습 과정
- 중심점 선택 : 랜덤
- 클러스터 할당 : K개의 중심점과 각 개별 데이터 간의 거리 측정 후, 가장 가까운 중심점 기준으로 데이터 할당, 클러스터는 덩어리 자체
- 새로운 중심점 선택
- 범위 확인 : 중심점의 더 이상 변화 없으면 진행 멈춤
K-Means는 아래와 같은 상황에 쓰지 말 것
데이터가 비선형
군집 크기가 다를 때
군집마다 밀집도와 거리가 다를 떄
Sum_of_squared_distances = []
K = range(1, 15)
for k in K:
km = KMeans(n_clusters = k)
km = km.fit(data_transformed)
Sum_of_squared_distances.append(km.inertia_)
plt.plot(K,Sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('optimal k')
plt.show()밀도 기반 군집 분석
- 사전에 클러스터의 숫자를 모를 때 사용하면 유용
- 이상치가 많이 포홤되었을때 사용하면 좋음
- 노이즈에 영향을 받지 않음
노이즈? 이상치?
노이즈 : 주어진 데이터셋과 무관하게 무작위성 데이터로 전처리 과정에서 제거해야 할 부분
이상치 : 관측된 데이터 범위에서 많이 벗어난 아주 작은 값이나 아주 큰 값
학습 과정
1. 엡실론 내 점 개수 확인 및 중심점 결정
- 점 P1에서 거리 엡실론 내에 점이 m(minPts) 개 있으면 하나의 군집으로 판단
- minPts =3 일 때 아래 그림에서 P1은 중심점
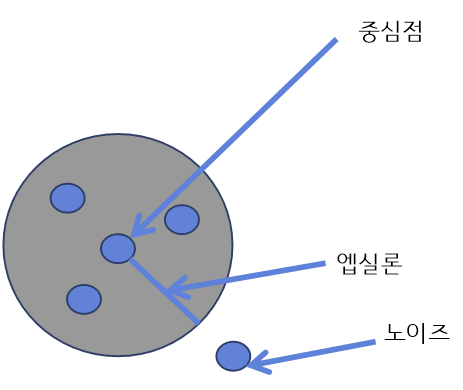
2. 군집 확장
- 1단계에서 군집 만들고 , 두 번째 군집을 생성
- 밀도가 높은 지역에서 중심점을 만족하는 데이터가 있다면 그 지역을 포함하여 새로운 군집 생성
- 그러고 하나의 군집으로 확대
3. 1~2단계 반복
4. 노이즈 정의 : 군집에 포함되지 않은 데이터를 노이즈로 정의
주성분 분석(PCA)
- 데이터 간소화
- 데이터 특성이 너무 많을 경우에는 데이터를 하나의 플롯에 시각화해서 살펴보는 것이 어려움
- 이 때 특성 p개를 두세 개 정도로 압축해서 살펴보고 싶을 떄 유용
- 고차원 데이터를 저 차원 데이터로 축소
절차
- 데이터들의 분포 특성을 잘 설명하는 벡터 두 개 선택
- 벡터 두 개를 위한 적정한 가중치를 찾을 때까지 학습
'Study > 딥러닝 텐서플로 교과서 - 길벗' 카테고리의 다른 글
| [Book]6. 합성곱 신경망 2 (0) | 2022.01.04 |
|---|---|
| [Book]5. 합성곱 신경망 1 (0) | 2022.01.02 |
| [Book]4. 딥러닝 시작 (0) | 2021.12.29 |
| [Book]2. 텐서플로 기초 (0) | 2021.12.25 |
| [Book]1. 머신러닝과 딥러닝 (0) | 2021.12.24 |



